切换至摄影模板
博文
数学家毫无自知之明——费马大定理证明了全世界数学家都是白痴 ... ... ... ... ... . ...
|||
摘要: 费马大定理是整个数学界全面溃败的标志性事物,是数论学科无视学术规则,无视上游学科“逻辑学”和“语言学”全面警告一意孤行,刚愎自用,自取灭亡的临终遗言。
费马大定理是一个主项为集合概念的命题,只能是对不同的变量n去一个个地解决,因为世界上所有的数学定理的主项都是普遍概念或者单独概念。世界上没有任何一个数学定理的主项是集合概念。
国际数学界对费马大定理的证明错误百出,一无是处!它不仅仅违反了三段论公理,还错误地使用反证法,反推时没有逆行传递性,表明整个国际数学界缺乏正确的逻辑思维。
并且,美国人英国人德国人也是不老实的,我告诉普林斯顿大学【数学年刊】编辑部安德鲁怀尔斯的错误,他们拒不发表,并且安德鲁怀尔斯和法尔廷斯也不出来公开承认错误。
费马大定理与黎曼猜想的主项都是集合概念,都是二阶逻辑问题(二阶逻辑问题参见本博客【黎曼猜想】),都是属于无法一次性证明的问题。(为什么要强调“概念”?高斯说“在数学中最重要的不是符号,而是概念”)。
关键词:费马大定理,集合概念,三段论公理
一,预备知识:数学命题的主项必须是普遍概念或者单独概念
全世界的数学定理的主项都是普遍概念或者单独概念,世界上没有任何一个数学定理的主项是集合概念。
1, 概念的種類
(1),單獨概念和普遍概念
a,單獨概念,反映獨一無二的概念,單獨概念的外延只有一個。例如,上海,孫中山,,,。它們反映的概念都是獨一無二的。數學中的單獨概念有“e”“Π”。“e是超越數”就是一個單獨概念的命題。
b,普遍概念,普遍概念反映的是一個對象以上的概念,反映的是一個“類”,這個詞項的內涵由為了包含在詞項外延所必須具有的事物的性質組成。就是说,普遍概念的每一个个体必然具有这个概念的基本属性。例如:工人,無論“石油工人”,“鋼鐵工人”,還是“中國工人”,“德國工人”,它們必然地具有“工人”的基本屬性。數學中的普遍概念有例如“素數”,“合數”,等。“素數無窮多”就是一個普遍概念的命題。數學證明對象全部都是普遍概念或者單獨概念。
a,集合概念反映的是集合體,這個詞項的外延由詞項所應用的事物集合組成,例如“中國工人階級”,集合體的每一個個體不是必然具備集合體的基本屬性,例如某一個“中國工人”,不是必然具有“中國工人階級”的基本屬性。集合概念的命題是不需要證明的,也是無法證明的,只能是歸納總結。
b,非集合概念(省略)。
 ,,經過一系列演算程式,使得這個假設解(反例)的費馬方程變成:
,,經過一系列演算程式,使得這個假設解(反例)的費馬方程變成:
 ,,.......(2)
,,.......(2)
他指出這裏實際上是一個橢圓方程:
 ,......(3)
,......(3)
注意,(3)式是一個普遍概念。所有的橢圓方程都具有這個性質。
橢圓曲線是域上虧格為1的光滑射影曲線,它的(仿射)方程,通常稱為維爾斯特拉斯方程,可以寫成(3)式。
三,错误的逻辑
看看那些所谓的数学家们是怎样推导的(费马大定理—一个困惑了世间智者358年的谜):
1,费马大定理有反例则弗赖椭圆曲线方程成立。
2,弗赖椭圆方程不能模形式化(肯.黎贝1985年证明了弗赖椭圆方程不能模形式化)。(肯黎贝)
3,谷山志村猜想断言每一个椭圆方程都可以模形式化。(谷山与志村)
上面的推理错误百出
结论:(只能得出,根据规则,前提中有一个是否定判断,结论只能是否定的)
1,弗赖方程不是椭圆方程(特称否定判断O)。
2,谷山志村猜想不能成立。
就是说,肯黎贝定理与谷山志村猜想只能有一个正确,一个错误,不会两个都是正确的。
因为2,
推理违反了演绎推理三段论的规则:
五,费马大定理与谷山志村猜想的关系
弗賴方程只有被模形式化,谷山—志村猜想才與費馬大定理是交叉關系,費馬大定理才可能有反例,並不是必然有反例。
如果弗賴方程不能模形式化,費馬大定理與谷山志村猜想是反对關係。
肯.黎贝定理(弗赖椭圆方程不能模形式化)与谷山志村猜想(每一个椭圆方程都可以模形式化)只能有一个是正确的,一个是错误的。
就是说,弗赖方程无论是否可以模形式化,都推不出费马大定理是成立或者不成立。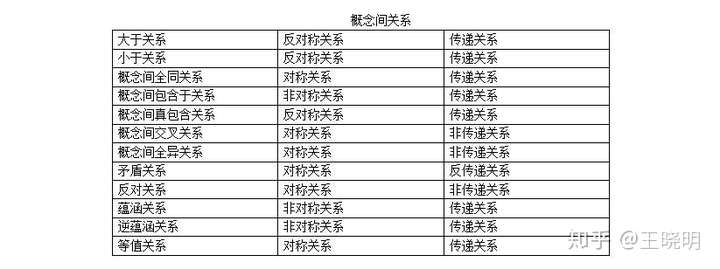
还有,费马大定理是无穷多个定理的集合,(n=2时叫做勾股定理)n=3时是一个定理,n=4时是一个定理,....。而不会有一个总定理,就是说没有一个集合概念的总定理。这是因为证实的局限性,证实只能增加一个可信度,而不能证明整个理论的正确性。看到了康托尔的厉害了吗?他认为无穷是有级别的。数学只能证明最低级别的无穷。
从费马大定理的被认可,我们看到了整个国际数学界思维混乱,数学界群体缺乏基本的逻辑训练,导致了数学在错误道路上运行。总之,重大数学问题不能由几个所谓“大师”说了算,必须由数学家逻辑学家语言学家共同鉴定。
七,给安德鲁怀尔斯鉴定的法尔廷斯也是错误的
数学不能放纵自己,数学要守规矩,数学必须自律。
最近几十年,数论成果大爆炸,实际上是错误信息大爆炸,数论成果是不会大爆炸的,因为,数论知识的产生成本是非常高的,数论存在了2000多年,成果就是这么一点点,以至于一个学习数论的学者都不可能错过任何知识。
关键词:费马大定理,集合概念,三段论公理
一,预备知识:数学命题的主项必须是普遍概念或者单独概念
全世界的数学定理的主项都是普遍概念或者单独概念,世界上没有任何一个数学定理的主项是集合概念。
1, 概念的種類
(1),單獨概念和普遍概念
a,單獨概念,反映獨一無二的概念,單獨概念的外延只有一個。例如,上海,孫中山,,,。它們反映的概念都是獨一無二的。數學中的單獨概念有“e”“Π”。“e是超越數”就是一個單獨概念的命題。
b,普遍概念,普遍概念反映的是一個對象以上的概念,反映的是一個“類”,這個詞項的內涵由為了包含在詞項外延所必須具有的事物的性質組成。就是说,普遍概念的每一个个体必然具有这个概念的基本属性。例如:工人,無論“石油工人”,“鋼鐵工人”,還是“中國工人”,“德國工人”,它們必然地具有“工人”的基本屬性。數學中的普遍概念有例如“素數”,“合數”,等。“素數無窮多”就是一個普遍概念的命題。數學證明對象全部都是普遍概念或者單獨概念。
(2),集合概念和非集合概念。
a,集合概念反映的是集合體,這個詞項的外延由詞項所應用的事物集合組成,例如“中國工人階級”,集合體的每一個個體不是必然具備集合體的基本屬性,例如某一個“中國工人”,不是必然具有“中國工人階級”的基本屬性。集合概念的命題是不需要證明的,也是無法證明的,只能是歸納總結。
b,非集合概念(省略)。
2,为什么数学证明的对象只能是普遍概念或者单独概念
这是因为数学家的武器级别都是一个“类”,即:定理,公理都是普遍概念,只能攻击同样级别的命题主项。而“集合概念”是一群类,是一群普遍概念。就好比一个人无法战胜一群敌人,而这个一群有可能是无穷多个类。
这是因为数学家的武器级别都是一个“类”,即:定理,公理都是普遍概念,只能攻击同样级别的命题主项。而“集合概念”是一群类,是一群普遍概念。就好比一个人无法战胜一群敌人,而这个一群有可能是无穷多个类。
这个问题也影响了希尔伯特第十问题:不定方程有无整数解的判定是否可行。增加了一个结论:主项是集合概念的命题不能证明是可以判定的。
二,費馬大定理的主项是什麼概念的命題
1,费马大定理是一个集合概念的命题
 .....(1)
.....(1)
對於>2的自然數,費馬說沒有 整數解,由於n=3, 4, 5, ...以致無窮,當然屬於集合概念,應該從=3,4, 5,....逐一證明。那麼,安德魯懷爾斯和其他数学家共同完成的证明是否成立?
1,费马大定理是一个集合概念的命题
對於>2的自然數,費馬說沒有 整數解,由於n=3, 4, 5, ...以致無窮,當然屬於集合概念,應該從=3,4, 5,....逐一證明。那麼,安德魯懷爾斯和其他数学家共同完成的证明是否成立?
2,转换命题
請注意他的證明方法,他證明的是:假如存在一個反例,注意,反例只要一個就夠了,格哈德.弗賴將方程(1)
請注意他的證明方法,他證明的是:假如存在一個反例,注意,反例只要一個就夠了,格哈德.弗賴將方程(1)
(弗赖)
轉換成為一個普遍概念的椭圆曲线方程:如果費馬大定理是錯誤的,那麼,至少有一個解,
他指出這裏實際上是一個橢圓方程:
注意,(3)式是一個普遍概念。所有的橢圓方程都具有這個性質。
橢圓曲線是域上虧格為1的光滑射影曲線,它的(仿射)方程,通常稱為維爾斯特拉斯方程,可以寫成(3)式。
三,错误的逻辑
看看那些所谓的数学家们是怎样推导的(费马大定理—一个困惑了世间智者358年的谜):
1,费马大定理有反例则弗赖椭圆曲线方程成立。
2,弗赖椭圆方程不能模形式化(肯.黎贝1985年证明了弗赖椭圆方程不能模形式化)。(肯黎贝)
3,谷山志村猜想断言每一个椭圆方程都可以模形式化。(谷山与志村)
上面的推理错误百出
因为1:
三段论:
大前提:(谷山——志村断言)每一个椭圆方程必然可以模形式化(全称肯定判断A)。
小前提:弗赖椭圆方程不能模形式化。(肯.黎贝证明了这个问题)
三段论:
大前提:(谷山——志村断言)每一个椭圆方程必然可以模形式化(全称肯定判断A)。
小前提:弗赖椭圆方程不能模形式化。(肯.黎贝证明了这个问题)
结论:(只能得出,根据规则,前提中有一个是否定判断,结论只能是否定的)
1,弗赖方程不是椭圆方程(特称否定判断O)。
2,谷山志村猜想不能成立。
就是说,肯黎贝定理与谷山志村猜想只能有一个正确,一个错误,不会两个都是正确的。
因为2,
推理违反了演绎推理三段论的规则:
大前提:否定费马大定理的反例-——弗赖椭圆曲线方程存在。【特称判断】。
小前提:弗赖椭圆方程不能模形式化(即弗赖方程不能成立)【否定判断】。
结论:费马大定理成立【全称肯定判断】。
根据逻辑规则:
1,如果大前提是特称判断,小前提是否定判断,不能得出结论。
2,在两个否定的前提中不能得出结论。
一共8条。
四,违反了三段论公理
国际数学界的上述推理违反了三段论公理。
根据,三段论公理:
凡是对一类事物性质有所肯定,则对该类事物中的每一个分子的性质也应该有所肯定;
凡是对一类事物性质有所否定,则对该类事物中的每一个分子的性质也应该有所否定。
从概念的外延方面看,
国际数学界的上述推理违反了三段论公理。
根据,三段论公理:
凡是对一类事物性质有所肯定,则对该类事物中的每一个分子的性质也应该有所肯定;
凡是对一类事物性质有所否定,则对该类事物中的每一个分子的性质也应该有所否定。
从概念的外延方面看,

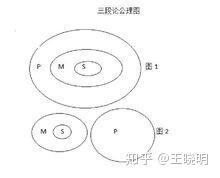
图1表示:s类包含于m类,m类包含于p类,所以,s类包含于p类;
图2表示:s类包含于m类,m类与p类全异,所以,s类与p类全异。
三段论公理的客观基础就是类与类的包含关系和全异关系,是人类亿万次重复实践中总结出来的不证自明的性质。
我们设图中的:
M 表示 ,,即(3)式;
,,即(3)式;
三段论公理的客观基础就是类与类的包含关系和全异关系,是人类亿万次重复实践中总结出来的不证自明的性质。
我们设图中的:
M 表示
S 表示  , 即(2)式,
, 即(2)式,
如果M具有性质P(模形式化),S却不具有性质P,得出了违反公理的结论。也说明了谷山志村猜想证明有错误。
好比说浙江省属于中国,杭州市属于浙江省,但是,杭州市不属于中国。
五,费马大定理与谷山志村猜想的关系
弗賴方程只有被模形式化,谷山—志村猜想才與費馬大定理是交叉關系,費馬大定理才可能有反例,並不是必然有反例。
如果弗賴方程不能模形式化,費馬大定理與谷山志村猜想是反对關係。
肯.黎贝定理(弗赖椭圆方程不能模形式化)与谷山志村猜想(每一个椭圆方程都可以模形式化)只能有一个是正确的,一个是错误的。
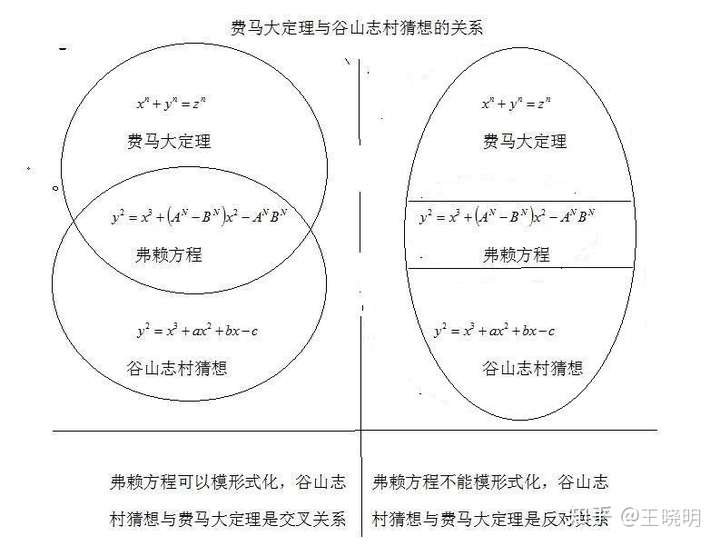
就是说,弗赖方程无论是否可以模形式化,都推不出费马大定理是成立或者不成立。
为什么?
因为:
概念间交叉关系,是一种对称关系,是一种非传递关系,谷山志村猜想对与错都不能传递到费马大定理的对与错;
概念间的反对关系是一种对称关系,是一种非传递关系,谷山志村猜想对与错都不能传递到费马大定理的对与错。
概念间交叉关系,是一种对称关系,是一种非传递关系,谷山志村猜想对与错都不能传递到费马大定理的对与错;
概念间的反对关系是一种对称关系,是一种非传递关系,谷山志村猜想对与错都不能传递到费马大定理的对与错。
(概念之间的关系是中国政府公务员历年考试题目,有1000万中国青年学习过这个内容,绝大多数考试的中国青年不会搞错,下面是概念之间逻辑关系)

六,概念的属性取决于当时的语境
一个词项是什么概念,取决于当时的语境,例如:
1,“费马大定理是很著名的数学问题”。这里的“费马大定理”属于单独概念。
2,“费马大定理是说n=3,4,5,...时没有整数解”。这里的“费马大定理”指集合概念。
一个词项是什么概念,取决于当时的语境,例如:
1,“费马大定理是很著名的数学问题”。这里的“费马大定理”属于单独概念。
2,“费马大定理是说n=3,4,5,...时没有整数解”。这里的“费马大定理”指集合概念。
还有,费马大定理是无穷多个定理的集合,(n=2时叫做勾股定理)n=3时是一个定理,n=4时是一个定理,....。而不会有一个总定理,就是说没有一个集合概念的总定理。这是因为证实的局限性,证实只能增加一个可信度,而不能证明整个理论的正确性。看到了康托尔的厉害了吗?他认为无穷是有级别的。数学只能证明最低级别的无穷。
从费马大定理的被认可,我们看到了整个国际数学界思维混乱,数学界群体缺乏基本的逻辑训练,导致了数学在错误道路上运行。总之,重大数学问题不能由几个所谓“大师”说了算,必须由数学家逻辑学家语言学家共同鉴定。
七,给安德鲁怀尔斯鉴定的法尔廷斯也是错误的
格尔德·法尔廷斯宣称证明莫德尔猜想,获得了菲尔兹奖,由莫德尔猜想推不出全称判断的费马大定理,所以,法尔廷斯推出特称判断的结论:
xⁿ+yⁿ=1,(n>3)上只有有限个有理点。”只有有限个有理点” 是一个特称判断,表现形式为:“有些A是B”。而一个数学定理要求:“一切A是B”。所以,法尔廷斯的结论不是一个定理,他的工作只是一个没有意义的探索,对于解决问题没有任何作用。 为什么法尔廷斯的结论是错误的?
原因是:我们首先需要知道有理点是 “有” 还是 “无”,法尔廷斯也不知道,他是说:我也不知道有没有这个有理点,我只能假定它,如果有,也是有限的。
现在明白了法尔廷斯的错误在哪里吗?
他犯了预期理由的错误:“假定费马曲线存在有理点”,就是引入了一个“加定存在”的非逻辑前提,这个错误使得后面的结论没有任何效力。
因为数学证明严禁引入非逻辑前提。
原因是:我们首先需要知道有理点是 “有” 还是 “无”,法尔廷斯也不知道,他是说:我也不知道有没有这个有理点,我只能假定它,如果有,也是有限的。
现在明白了法尔廷斯的错误在哪里吗?
他犯了预期理由的错误:“假定费马曲线存在有理点”,就是引入了一个“加定存在”的非逻辑前提,这个错误使得后面的结论没有任何效力。
因为数学证明严禁引入非逻辑前提。
1,假定。只能用在否定结果的证明中,例如,欧几里得证明素数无穷多个。
假定a成立,可以推出b,得到c,c与a矛盾,所以假定的a不能成立,得到非a。
2,假定不能用在肯定的结论。假定a,可以推出b,得到c,c=a,或者c包含a,所以假定的a成立。(这个就是预期理由的错误)
3,为什么“假定”只能用于否定的结论,而不能用于肯定的结论?
一个对科学理论更强的逻辑制约因素是,它们是能够被证伪的。换一句话说,因为以后能够被观测作有意义的检验,理论一定有被证伪的可能性。这种证伪的判据是区分科学与伪科学的一种方法。原因在于证实的内在局限性,证实只能增加一个理论的可信度,却不能证明整个理论的完全正确。因为在未来的某一个时刻,总是会发现与理论有冲突的事例。
费马大定理的n是一阶变化率,x、y、z是二阶变化率,对于二阶逻辑问题只能一个个解决,而无法一次性解决。
黎曼猜想也是二阶逻辑问题。
还有圆周率的计算以及自然对数的底e,都是二阶逻辑问题,没有人可以一次性计算出圆周率所有的小数或者小数规律。
数学不能放纵自己,数学要守规矩,数学必须自律。
最近几十年,数论成果大爆炸,实际上是错误信息大爆炸,数论成果是不会大爆炸的,因为,数论知识的产生成本是非常高的,数论存在了2000多年,成果就是这么一点点,以至于一个学习数论的学者都不可能错过任何知识。
八,结果
2016年我写信给证明费马大定理的团队,其中有普林斯顿大学【数学年刊】,肯黎贝,泰勒,牛津大学数学机构。2017年,安德鲁怀尔斯得知自己错误以后的照片,表情充满忧虑。显然,安德鲁怀尔斯已经接到消息,得知自己的错误,于是出现了这张充满忧虑的照片。
| 检测语言世界语中文简体中文繁体丹麦语乌克兰语乌兹别克语乌尔都语亚美尼亚语伊博语俄语保加利亚语信德语修纳语僧伽罗语克罗地亚语冰岛语加利西亚语加泰罗尼亚语匈牙利语南非祖鲁语卡纳达语卢森堡语印地语印尼巽他语印尼爪哇语印尼语古吉拉特语吉尔吉斯语哈萨克语土耳其语塔吉克语塞尔维亚语塞索托语夏威夷语威尔士语孟加拉语宿务语尼泊尔语巴斯克语布尔语(南非荷兰语)希伯来语希腊语库尔德语弗里西语德语意大利语意第绪语拉丁语拉脱维亚语挪威语捷克语斯洛伐克语斯洛文尼亚语斯瓦希里语旁遮普语日语普什图语格鲁吉亚语毛利语法语波兰语波斯尼亚语波斯语泰卢固语泰米尔语泰语海地克里奥尔语爱尔兰语爱沙尼亚语瑞典语白俄罗斯语科萨科西嘉语立陶宛语索马里语约鲁巴语缅甸语罗马尼亚语老挝语芬兰语苏格兰盖尔语苗语英语荷兰语菲律宾语萨摩亚语葡萄牙语蒙古语西班牙语豪萨语越南语阿塞拜疆语阿姆哈拉语阿尔巴尼亚语阿拉伯语韩语马其顿语马尔加什语马拉地语马拉雅拉姆语马来语马耳他语高棉语齐切瓦语 | 世界语中文简体中文繁体丹麦语乌克兰语乌兹别克语乌尔都语亚美尼亚语伊博语俄语保加利亚语信德语修纳语僧伽罗语克罗地亚语冰岛语加利西亚语加泰罗尼亚语匈牙利语南非祖鲁语卡纳达语卢森堡语印地语印尼巽他语印尼爪哇语印尼语古吉拉特语吉尔吉斯语哈萨克语土耳其语塔吉克语塞尔维亚语塞索托语夏威夷语威尔士语孟加拉语宿务语尼泊尔语巴斯克语布尔语(南非荷兰语)希伯来语希腊语库尔德语弗里西语德语意大利语意第绪语拉丁语拉脱维亚语挪威语捷克语斯洛伐克语斯洛文尼亚语斯瓦希里语旁遮普语日语普什图语格鲁吉亚语毛利语法语波兰语波斯尼亚语波斯语泰卢固语泰米尔语泰语海地克里奥尔语爱尔兰语爱沙尼亚语瑞典语白俄罗斯语科萨科西嘉语立陶宛语索马里语约鲁巴语缅甸语罗马尼亚语老挝语芬兰语苏格兰盖尔语苗语英语荷兰语菲律宾语萨摩亚语葡萄牙语蒙古语西班牙语豪萨语越南语阿塞拜疆语阿姆哈拉语阿尔巴尼亚语阿拉伯语韩语马其顿语马尔加什语马拉地语马拉雅拉姆语马来语马耳他语高棉语齐切瓦语 |
文本转语音功能仅限200个字符
免责声明:本文中使用的图片均由博主自行发布,与本网无关,如有侵权,请联系博主进行删除。
发表评论 评论 (3 个评论)
- 回复 wxmwrk
- https://docs.google.com/document/d/1I03oBlH20eWcSKMcL_c0MyGtIoYhMs-piH_-OAhTlpg/edit
100年以来对重大数论问题的证明都是错误的
- 回复 wxmwrk
- 2016年7月,发布在人民网,费马大定理内容,台湾和香港都有转载
http://bbs1.people.com.cn/post/1/1/2/157664469.html




